À moins d’avoir passé ces derniers mois dans une grotte au bout du monde (auquel cas vous n’êtes certainement pas entrain de lire cet article…), sinon vous n’avez pas pu échapper au flot d’informations sur l’épidémie de Covid-19. Une chose frappante, c’est la difficulté d’en modéliser l’évolution. Aux États-Unis par exemple le CHS dans un récent rapport s’en est alarmé lors d’un état des lieux des méthodes existantes et propose en conséquence la création d’un centre national de “outbreak science”, qu’on pourrait traduire par “science des irruptions épidémiques”. Certes des modèles de prévision existent, comme les fameuses prévisions de l’Imperial College. Mais force est de constater que, même au sommet de l’État, on ne semble pas être en mesure d’obtenir des prédictions précises. À l’instar du CHS, beaucoup constatent qu’il y a dans ce domaine encore beaucoup de progrès à faire. Chez Parcoor nous nous spécialisons dans les prévisions temporelles, et avons donc voulu apporter notre contribution dans ce domaine.
Le modèle CAST en deux mots…
En deux mots, le modèle CAST (pour Cell Agent State Transitions) modélise des agents qui se déplacent de cellule en cellule sur une map. Les cellules sont réparties à volonté sur la map. Chaque agent a sa home cell (“cellule maison”) qu’il peut partager ou non avec d’autres agents. La probabilité d’un agent de se déplacer dépend de sa propre mobilité et de la gravité de son état (plus son état est grave, moins il a de chance de se déplacer). S’il se déplace, c’est vers une cellule sélectionnée aléatoirement en fonction de sa distance à la home cell de l’agent et à son attractivité. Si un agent se retrouve dans la même cellule qu’un autre infecté, il peut se faire infecter lui-même (en fonction de sa sensibilité, de la contagiosité de l’agent infecté et de l’insûreté de la cellule). Une fois infecté, un agent passe d’état en état selon des transitions aléatoires et des durées. Ces probabilités de transitions et ces durées sont propres à chaque agent et fixées à l’avance.
Le but au final est d’avoir un modèle suffisamment réaliste tout en restant calculable sur un ordinateur grand public.
L’autre but est de pouvoir calculer l’impact de mesures sanitaires en modifiant des paramètres du modèle pendant la simulation. Par exemple en cas de confinement, on réduit fortement le paramètre de mobilité des agents sur la map. Si le port des masques est généralisé on réduit la contagiosité de ces agents. Etc.
Ici on se sert de ce modèle pour modéliser la propagation d’une maladie au sein d’une population, mais ce n’est pas son unique usage possible. On pourrait aussi imaginer par exemple simuler la propagation d’un virus informatique (les agents seraient alors des fichiers, les cellules seraient des serveurs etc.)
Moyennant cela, on lance une simulation et on observe ce qu’il se passe…
Exemple
On a lancé une simulation sur une map contenant 1000 agents et 600 cellules réparties aléatoirement sur une map. Concernant l’évolution spatio-temporelle du nombre de malades sur la map, voici ce qu’on obtient:

Chaque case pourrait représenter les régions ou département d’un pays.
Concernant l’évolution du nombre d’agents dans les différents états au cours du temps, on obtient ce graphique:
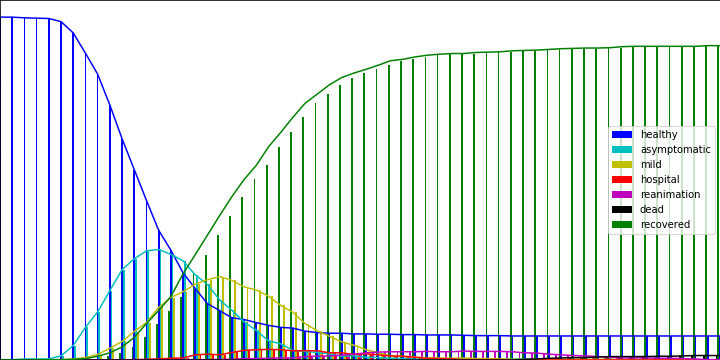
On s’aperçoit ici que le modèle retrouve “naturellement” le concept d’immunité collective après qu’une certaine proportion de la population ait été contaminée. “Naturellement”, car résultant de l’évolution de la simulation, sans que ça ait été paramétré.
L’implémentation du modèle CAST permet aussi de garder trace de qui a infecté qui, ce qu’on peut ensuite visualiser en plus de l’évolution entre états des agents:
Cette traçabilité de la chaîne de contamination permet ensuite de modéliser par exemple l’effet du contact tracing pour contenir l’épidémie.
Voir le notebook compagnon pour reproduire ces résultats.
Plus en détails…
Éléments de base
Ce modèle considère trois éléments de base
- Cellule. Une cellule contient aucun, un ou plusieurs agents à chaque instant. Elle a aussi une position (coordonnées euclidiennes sur un plan)
- Agent. Un agent est à chaque moment dans un et un seul état dans une et une seule cellule. La cellule où il est placé au départ est appelé sa home_cell ou cellule_base.
- État. Un état a une sévérité, contagiosité et une sensitivité prenant toutes des valeurs entre 0 et 1.
Contagion
Une contagion peut intervenir au sein d’une cellule, quand s’y retrouvent au même moment un agent sain et un agent contagieux (ayant une contagiosité >0). La probabilité que l’Agent_A contamine l’Agent_B, tous deux dans la même cellule est donnée par:
\[p = contagiousity(state(Agent_A)) \times sensitivity(state(Agent_B)) \times unsafety(cell)\]NB:
- Si plusieurs agents dans la même cellule sont contagieux, seul le plus contagieux est pris en compte pour calculer p.
- La unsafety (insûreté) d’une cellule mesure à quelle point elle est propice à des contagions (si les gens y sont serrés ou au contraire distanciés etc.)
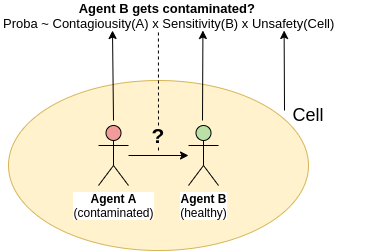
Si l’Agent_B se fait infecter, il passe à l’état ayant la plus faible sévérité strictement positive (il ne peut pas sauter directement à un état plus sévère).
Transitions d’états
Une matrice de transition d’états est attachée à chaque agent. Il s’agit d’un matrice markovienne décrivant les probabilités de transition d’un état à un autre. Chaque agent, s’il se retrouve dans un état, y reste pendant une durée fixée à l’avance qui lui est propre, avant de transitioner vers un autre état.
NB: Différents agents peuvent partager les mêmes états possibles et les mêmes matrices de transition, ou bien avoir la même matrice de transition mais des durées d’état différentes etc. On peut par exemple partager les agents en groupes de populations partageant la même matrice de transition, avec des durées d’état tirées de la même distribution de probabilité.
Mouvements
Un mouvement consiste en un agent se déplaçant vers une autre cellule. À chaque ronde, tous les agents sont concernés par les mouvement, mais seuls certains vont effectivement se déplacer. Cela se passe en deux étapes
- Sélectionner les agents qui vont se déplacer
- Déplacer les agents vers leur nouvelle cellule
Sélection des agents
Lors d’une ronde, la probabilité d’un agent de se déplacer est déterminer:
\[p = proba\_move(agent) \times (1 - severity(state(agent)))\]Le premier facteur représente la mobilité d’un agent. Le second représente le fait que plus la sévérité de l’état d’un agent es grande, moins il est probable qu’il se déplace
Sélection des cellule
La cellule où déplacer un agent sélectionné pour un mouvement à l’étape précédente est choisie aléatoirement selon la probabilité:
\[p \~{} \frac{attractivity(cell)}{distance(home\_cell(agent), cell)}\]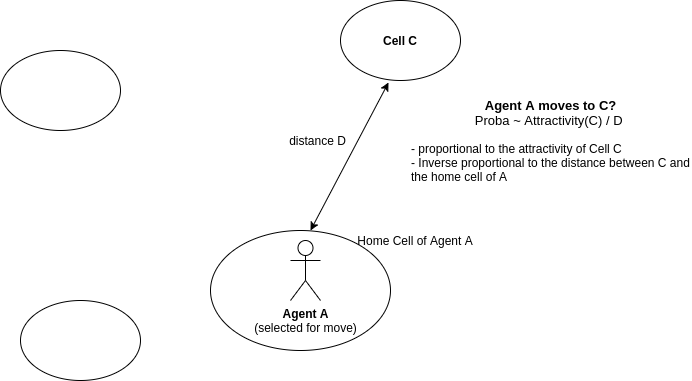
NB:
- Une limitation de ce modèle est que l’attractivité de chaque cellule est la même pour tous les agents.
- La distance est toujours calculée depuis la home_cell de l’agent. On donc considère qu’un agent se déplace autour de sa home cell.
- Un agent qui n’est pas sélectionné pour un mouvement retourne alors dans sa home_cell.
Chronologie
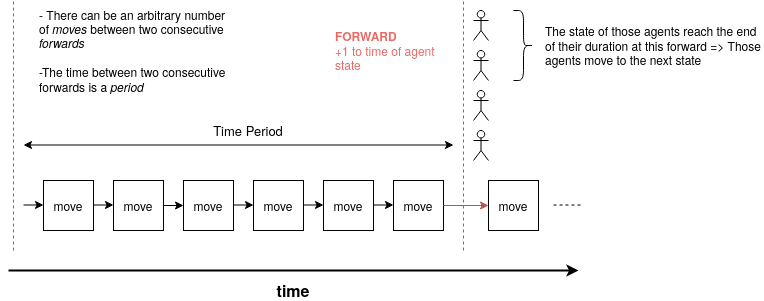
Chaque période est faite d’un certain nombre de rondes de mouvements. Ce nombre de rondes peut être différent pour chaque période. Durant chaque ronde, les agents se déplacent comme décrit précedemment. S’ils sont infectés, ils peuvent alors infectés d’autres agents se retrouvant dans la même cellule après une ronde de mouvement. À la fin de chaque période, tous les agents sont forwardés, c’est à dire que la durée de l’état dans lequelle il se trouve est incrémentée de 1. Si cet état a une durée finit et qu’elle arrive alors à expiration, l’agent passe à un autre état selon sa matrice de transition.
Perspectives
Même si l’implémentation actuelle est assez performante (grâce notamment à l’utilisation intensive de librairies comme numpy), la performance pourrait être encore grandement améliorée en utilisant du calcul GPU, rendant alors possible de simuler des propagations sur de larges populations rapidement. D’autres affinements sont possible, comme par exemple une attractivité des cellules différenciée selon des catégories de population. Certaines cellules par exemple pourraient être beaucuop plus attractives pour les jeunes que pour les personnes âgées et inversement.
En conclusion, même si ce modèle n’est sans doute pas la solution ultime, on pense qu’il est capable de fournir des prévisions utiles en cas d’épidémies, de simuler l’impact de mesures sanitaires, et ainsi d’apporter sa pierre à l’outbreak science émergente.